
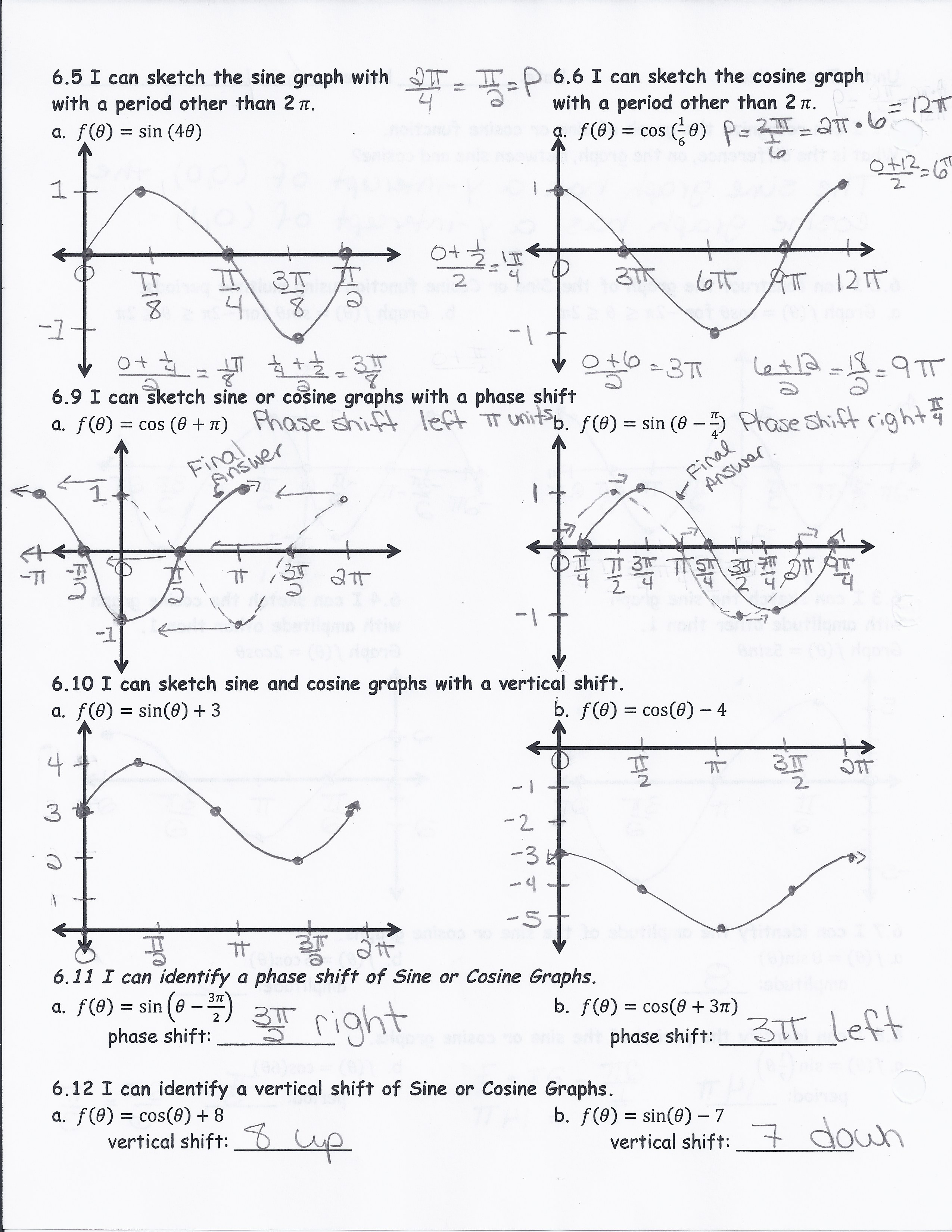
sin(x) is zero is unaffected by the value of the parameter a.
The point at which the value of the function y = a This makes intuitive sense when some functions are set equal to zero and evaluated over the domain x = (0, π] However, it is important to note that the points of intersection with the x-axis are not changed.

The distance from the x-axis to the peak of the trough seems to correspond to the value of the parameter a, eg: the peak of the trough of the sine curve is |a| from the x-axis. To this end we will examine several different values for parameter a in the sin function y = a sin x below are illustrations of y = 1 sin x, y = 2 sin x, and y = 3 sin x, and y = 4 sin x In this micro investigation we are interested in developing a mathematical interpretation of the effect of varying the value of parameter a on the curve y = a sin (bx + c). Micro-investigation 1: Varying the value of parameter a values of parameter b = 1 and parameter c = 0 held constant. What were to happen to the curve if we manipulated the values of each of the parameter values individually? Let's investigate for the curve y = a sin (bx + c) This visualization shows a sine curve with parameter values of a = 1, b = 1, and c = 0. The graph of the function y = sin x is shown below for reference. Perhaps initailly not as intuitive as linear functions, understanding the effects of changing parameter values a, b, and c on the sine function y = a sin (bx + c) can be developed using programs such as Graphing Calculator or Desmos. Provide a mathematical interpretation of the Parameters a, b, and, c.Įxplore using animations to illustrate the impact of each parameter. The Function of a Sine Curve and the Nature of its ParametersĮxamine graphs of y = a sin(bx + c) for different values of a, b, and c.


 0 kommentar(er)
0 kommentar(er)
